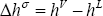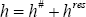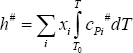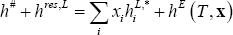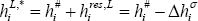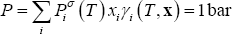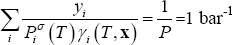Chapter 4:
From Phases to Method (Models) Selection
Abstract
Read the abstractTable of contents
See the table of contentsList of examples
- 4-1: Calculation of the condensation enthalpy of the acetone + water mixture with NRTL at a given pressure (1 bar)
- 4-2: Distribution coefficients in an ideal mixture (propane + n-pentane)
- 4-3: Comparison of phase envelope predictions for the ethane + n-pentane mixture
- 4-4: Behaviour of a methane + n-decane mixture and its models
- 4-5: Behaviour of the benzene + n-hexane mixture and its models
- 4-6: Calculation of the eutectic of para- and ortho-xylene
- 4-7: Comparison of experimental values and different model with H2 + n-hexane mixture
- 4-8: Prediction of a heteroazeotrope with total liquid immiscibility
- 4-9: Formation of hydrates
- 4-10: Example of a vapour-liquid-liquid equilibrium of an acid gas system in the presence of water
- 4-11: VLE and LLE calculation of the methanol + n-hexane mixture
Example 4-1: Calculation of the condensation enthalpy of the acetone + water mixture with NRTL at a given pressure (1 bar)
Analysis:
The condensation enthalpy is required. This is the difference between the vapour and liquid enthalpy of a mixture:
Since vapour enthalpy is always larger than liquid enthalpy, this number is always positive. The vaporization enthalpy has the opposite sign and is therefore always negative.
The enthalpy of a phase is calculated using the ideal gas and the residual contribution.
The ideal gas contribution is calculated using the ideal gas heat capacity of the individual components and the knowledge that the ideal gas is an ideal mixture:
In this equation, the reference enthalpy is taken to be zero in the thermodynamic state defined as the pure component ideal gas at temperature T0. The pressure of the reference state need not be stated since pressure has no effect on the ideal gas enthalpy.
The residual contribution to equation (2) can be neglected in the vapour phase (pressure less than 5 bar), and calculated in the liquid phase using either an equation of state or an excess energy model. In the latter case, the pure component residual contributions must be known through another means. In this example, the mixture (acetone + water) behave in a strongly non-ideal manner, and it is therefore recommended to use an excess Gibbs energy model. It is possible to calculate the excess enthalpy from the excess Gibbs energy using the Gibbs-Helmholtz relationship. The NRTL excess energy model is proposed (introduced in section 3.4.2.2.C). The liquid phase residual enthalpy can be calculated as:
where the pure component liquid enthalpies should be computed using the same reference state as for the vapour state (as in equation (2)):
where the pure component residual enthalpy is assumed to be equal to be the opposite of the vaporization enthalpy. This assumption is acceptable provided that the saturated vapour behaves as an ideal gas at the temperature of interest.
Note that for a mixture, the temperature of the dew and the bubble point are different. Therefore, the temperature at which 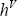 and
and 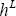 should be calculated are different. These temperatures are also calculated using the NRTL method, through the activity coefficients:
should be calculated are different. These temperatures are also calculated using the NRTL method, through the activity coefficients:
- for the bubble point, the temperature must be found from solving following equation, at given composition (x):
- for the dew point, the temperature must be found from solving following equation, at given composition (y):
In this last equation, x must be computed at each iteration from the phase equilibrium equations.
Solution:
See complete results in file (xls):
Some help on nomenclature and tips to use this file can be found here.
From the above equations, it is clear that many different models come into play before the actual condensation enthalpy can be calculated:
- Ideal gas isobaric heat capacity for each component,
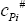
- Vaporisation enthalpy for each component,
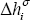
- Vapour pressure for each component,
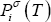
- The NRTL equation that is used both for calculating activity coefficients,
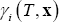 and excess enthalpy,
and excess enthalpy, 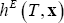 .
.
Each of these models should be validated against experimental data.
The excel sheet provides the results in tabular form.
The bubble and dew temperatures calculated from equations (6) and (7) are shown in Figure 1. To calculate the condensation enthalpy of a pure component, therefore, we can write:
- Calculate the ideal gas enthalpies at the dew temperature, using equation (2), columns D and E for each component; column F for the mixture. Considering the low pressure conditions, this may be considered as the vapour phase enthalpy.
- Calculate the ideal gas enthalpies at the bubble temperature, using equation (4), columns H and I for each component; column J for the mixture.
- Calculate the vaporisation enthalpy at the bubble temperature, for each pure component, columns K and L in the Excel sheet.
- Calculate the excess enthalpy for the mixture at the bubble temperature, column M.
- Use equations (3) and (2) for calculating the liquid phase enthalpy, column N.
The difference between the vapour and liquid phase enthalpies is the vaporisation enthalpy, shown in figure 2.
It is worth observing that the excess enthalpy is very small compared to the vaporization enthalpy. Neglecting the excess enthalpy results in over-estimating the vaporization enthalpy by 1 to 2%.
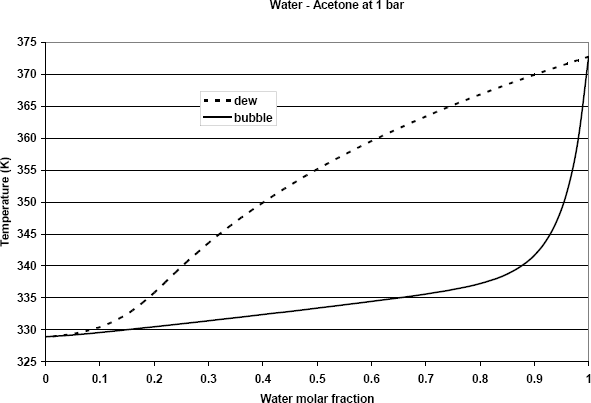 Figure 1: Dew and bubble temperature of the water + Acetone mixture as a function of composition.
Figure 1: Dew and bubble temperature of the water + Acetone mixture as a function of composition.
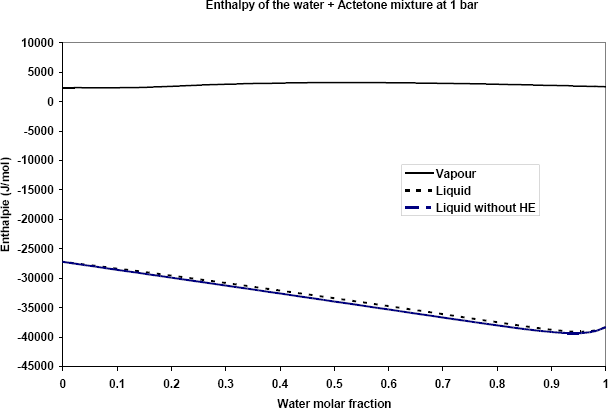 Figure 2: Liquid and vapour enthalpy of the water + acetone mixture at 1 bar. The difference between the two enthalpies is the vaporization enthalpy.
Figure 2: Liquid and vapour enthalpy of the water + acetone mixture at 1 bar. The difference between the two enthalpies is the vaporization enthalpy.