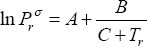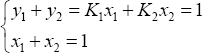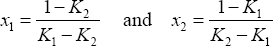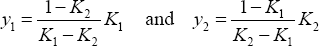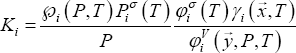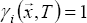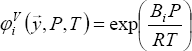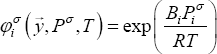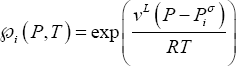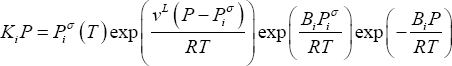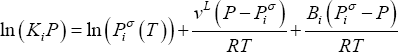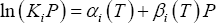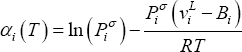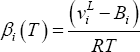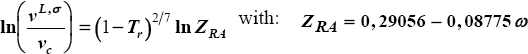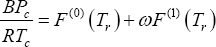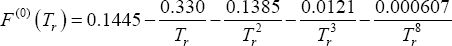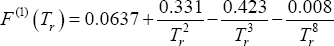Chapter 4:
From Phases to Method (Models) Selection
Abstract
Read the abstractTable of contents
See the table of contentsList of examples
- 4-1: Calculation of the condensation enthalpy of the acetone + water mixture with NRTL at a given pressure (1 bar)
- 4-2: Distribution coefficients in an ideal mixture (propane + n-pentane)
- 4-3: Comparison of phase envelope predictions for the ethane + n-pentane mixture
- 4-4: Behaviour of a methane + n-decane mixture and its models
- 4-5: Behaviour of the benzene + n-hexane mixture and its models
- 4-6: Calculation of the eutectic of para- and ortho-xylene
- 4-7: Comparison of experimental values and different model with H2 + n-hexane mixture
- 4-8: Prediction of a heteroazeotrope with total liquid immiscibility
- 4-9: Formation of hydrates
- 4-10: Example of a vapour-liquid-liquid equilibrium of an acid gas system in the presence of water
- 4-11: VLE and LLE calculation of the methanol + n-hexane mixture
Example 4-2: Distribution coefficients in an ideal mixture (propane + n-pentane)
Describe the impact of pressure on the phase compositions of an ideal mixture. As an example, we use the propane + pentane mixture at 343.15 K. Following data are available (Table 1). The A, B and C parameters are those used for the Antoine equation for calculating the vapour pressure expressed in non-dimensional units (  and
and  ):
):
| C3 | C5 | |
|---|---|---|
| Tc(K) | 369.8 | 469.6 |
| Pc(MPa) | 4.24866 | 3.37662 |
| Zc | 0.281 | 0.262 |
| Acentric factor | 0.152 | 0.251 |
| A | 5.7544 | 6.0008 |
| B | -5.4826 | -5.5603 |
| C | -0.0472 | -0.0734 |
Analysis:
Phase equilibrium for a binary mixture is calculated from the distribution coefficients, as follows:
yielding:
and therefore
If equilibrium is considered at high pressure, fugacity coefficients and Poynting corrections must be taken into account:
Assuming an ideal mixture (i.e. the equilibrium coefficient is independent of composition), the activity coefficient equals one:
In expression (4), the fugacity coefficients are approximated with that of the virial equation:
and
The Poynting correction is written as:
Introducing (8), (7) and (6) into (4), one finds:
which may be written as:
or:
where:
and
The distribution coefficients thus depend only on pure component properties (liquid molar volume  , vapour pressure
, vapour pressure  and second virial coefficient
and second virial coefficient  ). Equation (11) shows that the product of equilibrium constant and pressure should be considered. Raoult's law suggests that this product is only a function of temperature. In practice, a linear relationship with pressure is required above 0.5 MPa.
). Equation (11) shows that the product of equilibrium constant and pressure should be considered. Raoult's law suggests that this product is only a function of temperature. In practice, a linear relationship with pressure is required above 0.5 MPa.
Solution:
See complete results in file (xls):
Some help on nomenclature and tips to use this file can be found here.
In order to use the above equations, values for vapour pressure, liquid molar volume and second virial coefficient are needed. Unless specific parameters are provided, we use the corresponding states methods:
for vapour pressure, the Antoine parameters are provided
for liquid molar volume, the Rackett equation is used:
for second virial coefficient, the method of Tsonopoulos is used:
with:
and:
Phase equilibrium can now be computed from (2) and (3) using either the basic Raoult equation or the more complete equation (11). The results are as follows:
| P(MPa)= | 0.5 | |
|---|---|---|
| Ki Raoult | 5.3062 | 0.5780 |
| x | 0.0893 | 0.9107 |
| y | 0.4736 | 0.5264 |
| Ki (11) | 3.9161 | 0.6209 |
| x | 0.1151 | 0.8849 |
| y | 0.4506 | 0.5494 |
We can notice that the complete equation yields smaller distribution coefficients than the Raoult approximation if the value is larger than one, and larger distribution coefficients if it is smaller than one. This results in smaller differences in volatilities, and as a result phase compositions that are less different.
The distribution coefficients as a function of pressure for propane and n-pentane at 343.15 K are shown in figure 1. We can see that their respective slopes are such that the equilibrium coefficients converge at higher pressures. The practical meaning of this observation is that the volatility of the two components becomes closer when pressure is increased, and therefore more equilibrium stages will be needed to reach the same separation level.
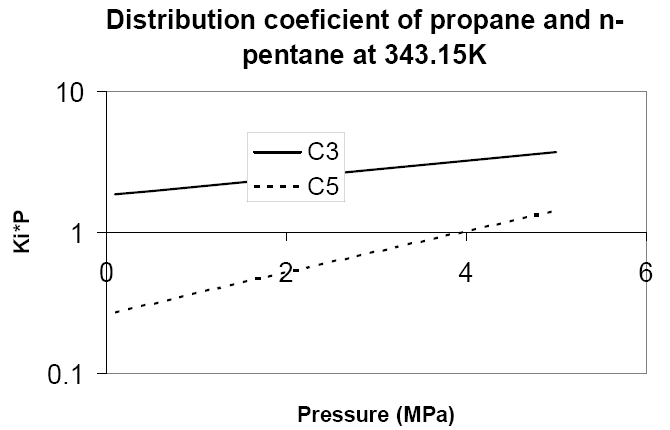 Figure 1: Change of propane and n-pentane equilibrium coefficients at 343.15K with pressure
Figure 1: Change of propane and n-pentane equilibrium coefficients at 343.15K with pressure