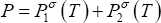Chapter 4:
From Phases to Method (Models) Selection
Abstract
Read the abstractTable of contents
See the table of contentsList of examples
- 4-1: Calculation of the condensation enthalpy of the acetone + water mixture with NRTL at a given pressure (1 bar)
- 4-2: Distribution coefficients in an ideal mixture (propane + n-pentane)
- 4-3: Comparison of phase envelope predictions for the ethane + n-pentane mixture
- 4-4: Behaviour of a methane + n-decane mixture and its models
- 4-5: Behaviour of the benzene + n-hexane mixture and its models
- 4-6: Calculation of the eutectic of para- and ortho-xylene
- 4-7: Comparison of experimental values and different model with H2 + n-hexane mixture
- 4-8: Prediction of a heteroazeotrope with total liquid immiscibility
- 4-9: Formation of hydrates
- 4-10: Example of a vapour-liquid-liquid equilibrium of an acid gas system in the presence of water
- 4-11: VLE and LLE calculation of the methanol + n-hexane mixture
Example 4-8: Prediction of a heteroazeotrope with total liquid immiscibility
Describe the conditions at which the benzene(1) + water(2) binary mixture form three distinct phases at 1 atm (0.10135 MPa) pressure. Give the phase compositions.
Analysis:
When considering only the moderate temperature region (i.e. well below the water critical point), a number of simple approximations can be made:
- The hydrocarbons and water are entirely insoluble in each other in the liquid phase.
- The vapour phase is an ideal gas.
- The vapour pressures may be obtained using the Antoine equation:
where Pσ is expressed in torr and T in °C
| A | B | C | |
|---|---|---|---|
| Benzene | 6.90565 | -1211.033 | 220.79 |
| Water | 7.96681 | -1668.21 | 228.0 |
The Gibbs phase rules states:
There are two components and three phases in the heteroazeotropic point, therefore only one degree of freedom. If pressure is fixed, the solution is defined.
Solution:
See complete results in file (xls):
Some help on nomenclature and tips to use this file can be found here.
The diagram is constructed starting from the pure components. The boiling temperature of benzene is 353.15 K, that of water 373.15 K. At low temperature, two liquid phases are present, whose compositions are known:
for the hydrocarbon phase: x1HC=1, x2HC=0 and
for the aqueous phase: x1aq=0, x2aq=1.
When the vapour is in equilibrium with the aqueous phase, we have:
This is the water dew curve (y1 vs T). Note that  .
.
When the vapour is in equilibrium with the hydrocarbon phase, we have:
This is the organic dew curve (y2 vs T). Note that  .
.
When the vapour is in equilibrium with both aqueous and organic liquids, both equations (2) and (3) are true simultaneously. They can be summed to yield:
The total three phase pressure is equal to the sum of the two vapour pressures. Only one temperature satisfies this condition for P = 1 atm, that is T = 69.12 °C (342.27 K). At this temperature, the vapour phase composition can be calculated: y2=0.3
Two dew curves are thus constructed. They meet at the three-phase point. The diagram is shown in figure 1.
 Figure 1: Benzene + water heteroazeotrope Txy diagram at 1 atm.
Figure 1: Benzene + water heteroazeotrope Txy diagram at 1 atm.