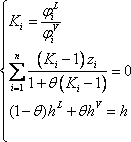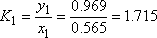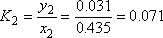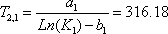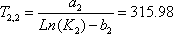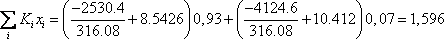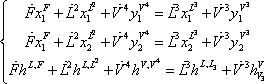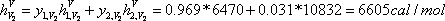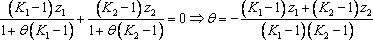Chapter 2:
From Fundamental to Properties
Abstract
Read the abstractTable of contents
See the table of contentsList of examples
- 2.1: Refrigeration system
- 2.2: VLE observation
- 2.3: Flexfuel model
- 2.4: Phase envelope of a natural gas with retrograde condensation
- 2.5: Entropy rise in a ideal gas expansion
- 2.6: Cryogenic plant
- 2.7: Distillation column
- 2.8: Energy balance in a column feed
- 2.9: Risk of condensation of water in a gas stream
- 2.10: Effect of the feed composition on the water-gas shift reaction
- 2.11: Effect of temperature on the reaction constant
- 2.12: Chemical looping
Example 2.8: Energy balance in a column feed
An adiabatic distillation column is used to separate a mixture of n-butane (1) and n-heptane (2). The liquid feed is introduced directly on the third stage as shown on figure 1.
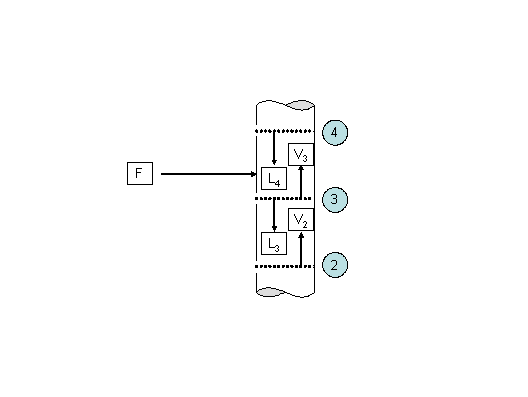 Figure 1 Energy balance in a column feed
Figure 1 Energy balance in a column feed
The column operates at an isobaric pressure of 2.26 atm. Some additional pieces of information concerning the characteristics of the feed and the surrounding stages are also given as follows:
| Position | Feed | Stage 2 | Stage 4 |
|---|---|---|---|
| Temperature (°C) | 47.5 | ||
| Vapour molar flow (mol/s) | 0 | 43.5 | |
| Liquid molar flow (mol/s) | 100 | 0.46 | 118.2 |
| Vapour molar composition y1 | 0.5 | 0.565 | 0.990 |
| Liquid molar composition x1 | 0.969 |
For the simplicity of the model, some basic expressions have been selected for enthalpy calculation and for distribution coefficient predictions: the expressions are 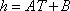 (with T in °C, and h in cal/mol) for both phases and
(with T in °C, and h in cal/mol) for both phases and 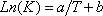 (with T in K). These equations apply to each component and the values of the coefficients are found below:
(with T in K). These equations apply to each component and the values of the coefficients are found below:
| Vapour enthalpy | Liquid enthalpy | Equilibrium constant | ||||
|---|---|---|---|---|---|---|
| Component | 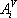 |
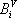 |
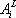 |
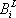 |
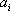 |
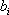 |
| n-Butane | 23.3 | 5470 | 34 | 0 | -2530.4 | 8.5426 |
| n-Heptane | 39.7 | 9128 | 54 | 0 | -4124.6 | 10.412 |
- What is the temperature of stage number 2?
- What is the temperature of stage number 4?
- What are the temperature and compositions of stage number 3?
Analysis:
The properties to be evaluated are the temperature of the various equilibria on the 3rd stage around the feed. Pressure is fixed and part of the compositions is given.
- a) For the 2nd stage the liquid and vapour composition are known, so the distribution equilibrium are directly obtained. The temperature can be calculated using the relationship between Ki and T.
- b) For the 4th stage, composition of liquid is known meaning that a bubble temperature point has to be determined.
- c) On the 3rd stage, all incoming flows are known, so the overall composition is known as the total enthalpy may be calculated. A PH flash must be solved using the set of following equations:
The fluids are regular light hydrocarbons. All properties are well known. Particular expressions are recommended and no binary interaction is considered (ideal mixture, i.e. 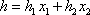 ).
).
All fluids will be found in both phases as vapour or liquid due to the under-critical pressure zone.
Solution:
See complete results in file (xls):
Some help on nomenclature and tips to use this file can be found here.
Plate number 2 is defined in both phases. So the distribution coefficients of each component can be calculated (it is a binary mixture!).
and
Normally, knowledge of T on the 2nd stage will give both 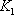 and
and 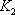 , so there are two equations for one unknown. Both equations lead to:
, so there are two equations for one unknown. Both equations lead to:
and
.The average is 316.08.
For the 4th stage, the bubble calculation has to be undertaken. The iterative procedure must start with an initial value (perhaps the temperature of stage number 2, or any other chosen by the user). If the temperature of stage 2 is used, equation 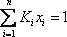 yields
yields
The temperature must be lowered to reduce the sum. After a few iterations, a value of 298.66 K is found for plate number 4.
Material and energy balances around the 3rd stage must be made.
This implies that enthalpies of each flow must be calculated. For example, the enthalpy of the vapour leaving stage 2, it is expressed by:
Using this technique, the material and enthalpy content of each of the streams entering the 3rd plate can be calculated and summed as shown in table 3.
| Component |  |
 |
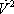 |
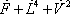 |
|---|---|---|---|---|
| n-Butane (mol/s) | 50 | 42.15 | 109.93 | 202.08 |
| n-Heptane (mol/s) | 50 | 1.35 | 8.27 | 59.62 |
| Total nC4+nC7 | 100 | 43.5 | 118.2 | 261.7 |
| h (cal/mol) | 2090 | 6605 | 903 | 2303 |
| H (cal/s) | 209000 | 287336 | 106740 | 603077 |
Introducing the equilibrium condition in the above material balances (2 first equations), they can be treated as mass balance leading to the Rachford Rice equation. For a binary mixture, the vapour fraction can be calculated directly:
We are now left with two equations (the enthalpy balance and the above Rachford Rice equation) with two unknowns (θ and T). The complete algorithm becomes very simple:
- Assume a temperature
- Calculate K1 and K2
- Solve the Rachford Rice equation to find θ
- Calculate the enthalpies of streams V3 and L3
- Compare the sum of these two outlet enthalpies with the inlet enthalpy calculated in table 3.
A complete iteration is shown in table 4.
a total enthalpy of 989.444 kcal/s
| Temperature (°C) = 40 | 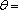 0.4366 0.4366 |
|||||||
|---|---|---|---|---|---|---|---|---|
| Component | 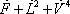 |
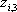 |
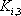 |
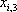 |
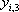 |
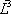 |
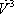 |
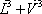 |
| n-Butane (mol/s) | 202.08 | 0.772 | 1.587 | 0.615 | 0.976 | 90.62 | 111.46 | 202.08 |
| n-Heptane (mol/s) | 59.62 | 0.228 | 0.063 | 0.385 | 0.024 | 56.83 | 2.79 | 59.62 |
| Total nC4+nC7 | 261.7 | 1 | 1 | 1 | 147.45 | 114.25 | 261.7 | |
| h (cal/mol) | 1668 | 6507 | 3781 | |||||
| H (cal/s) | 603077 | 246002 | 743442 | 989444 | ||||
As observed in the results above, calculated at a temperature of 40 °C, the vapour fraction of the flash is 0.4366 and the total enthalpy of 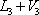 is 989444, greater than the value of 603077 for
is 989444, greater than the value of 603077 for 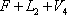 . The temperature must therefore be less than 40 °C. A few additional iterations lead to a final value of 34.29 °C with the corresponding compositions and vapour fraction as seen below:
. The temperature must therefore be less than 40 °C. A few additional iterations lead to a final value of 34.29 °C with the corresponding compositions and vapour fraction as seen below:
| Temperature (°C) = 34.29 | 0.1904 | |||||||
|---|---|---|---|---|---|---|---|---|
| Component | 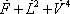 |
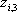 |
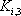 |
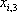 |
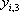 |
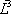 |
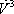 |
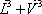 |
| n-Butane (mol/s) | 202.08 | 0.772 | 1.367 | 0.722 | 0.986 | 152.93 | 49.15 | 202.08 |
| n-Heptane (mol/s) | 59.62 | 0.228 | 0.050 | 0.278 | 0.014 | 58.94 | 0.69 | 59.62 |
| Total nC4+nC7 | 261.7 | 1 | 1 | 1 | 211.87 | 49.84 | 261.7 | |
| h (cal/mol) | 1357 | 6327 | 2303 | |||||
| H (cal/s) | 603077 | 287442 | 315209 | 603077 | ||||