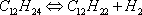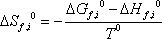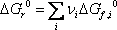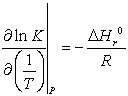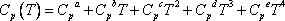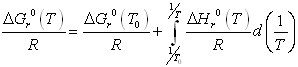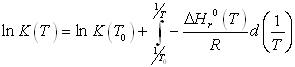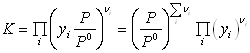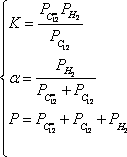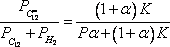Chapter 2:
From Fundamental to Properties
Abstract
Read the abstractTable of contents
See the table of contentsList of examples
- 2.1: Refrigeration system
- 2.2: VLE observation
- 2.3: Flexfuel model
- 2.4: Phase envelope of a natural gas with retrograde condensation
- 2.5: Entropy rise in a ideal gas expansion
- 2.6: Cryogenic plant
- 2.7: Distillation column
- 2.8: Energy balance in a column feed
- 2.9: Risk of condensation of water in a gas stream
- 2.10: Effect of the feed composition on the water-gas shift reaction
- 2.11: Effect of temperature on the reaction constant
- 2.12: Chemical looping
Example 2.11: Effect of temperature on the reaction constant
Calculate the equilibrium of the dodecane dehydrogenation reaction as a function of temperature, at a total pressure of 3 bar and a molar ratio of H2/HC of 6:
Analysis:
Required properties:
Pressure is known. The system composition must be calculated as a function of temperature (which is therefore known). In order to apply the chemical equilibrium, two types of properties must be computed: fugacities and Gibbs energy of reaction at the reference state.
Mixture:
- It is considered here that only hydrogen and hydrocarbons are of interest.
- The hydrogen pure component properties are readily available in any database.
- This may not always be the case for the long chain alkanes and alkenes. The n-dodecane and n-dodecene molecules are available in the DIPPR database that is used here. Use of a group contribution model will also be illustrated since it may be of interest for long-chain molecules.
- Although the molar mass of the components are very different, all are non-polar. We consider that the mixture is ideal for this example. This is justified below.
Phase condition:
In this example, the main argument for the choice of the fugacity model is based on the observation that the pressure is low and that in the reaction condition the mixture is in its vapour phase. Under these conditions, the ideal gas approximation can be used and the fugacities written as partial pressures (hence ideal mixture behaviour).
Solution:
See complete results in file (xls):
Some help on nomenclature and tips to use this file can be found here.
In order to calculate the equilibrium constant, the component formation properties are required. Table 1 provides these values as found in the DIPPR database.
| Component | 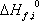 (kJ/mol) (kJ/mol) |
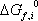 (kJ/mol) (kJ/mol) |
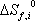 (kJ/(mol.K) (kJ/(mol.K) |
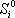 (kJ/(mol.K) (kJ/(mol.K) |
|---|---|---|---|---|
| n-dodecane | -290.7 | 49.81 | -1.1443 | 0.62415 |
| 1-dodecene | -165.4 | 136.1 | -1.0139 | 0.6185 |
| Hydrogen | 0 | 0 | 0 | 0.13057 |
Note that the entropy of formation is not given by the database, but that it is here calculated using the relationship with enthalpy and Gibbs energy:
These values are different from the absolute entropy that is also provided in the database (here given as S0 but not used).
Since gaseous hydrogen is considered as the component that represents the element H, its formation properties are zero by definition.
Using the Gibbs energies of formation:
we can now calculate the Gibbs free energy of reaction at 298.15 K: 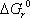 = 86.74 kJ/mol, and therefore the equilibrium constant:
= 86.74 kJ/mol, and therefore the equilibrium constant: 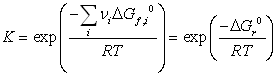
ln K = -34.99. This value is very small, indicating that at room temperature, the reaction equilibrium is such that the alkane is much more stable than the alkene. To observe dehydrogenation, the temperature must be raised, as demonstrated by the positive heat of reaction 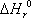 = 125.26 kJ/mol (indicating an endothermic reaction: the higher the temperature, the larger the conversion).
= 125.26 kJ/mol (indicating an endothermic reaction: the higher the temperature, the larger the conversion).
The temperature-dependence of the equilibrium constant is written according to
where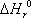 itself depends on temperature according to
itself depends on temperature according to 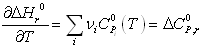 . This is why the ideal gas heat capacity of the components must be taken into account. Using the model of Passut & Danner (see chapter 3):
. This is why the ideal gas heat capacity of the components must be taken into account. Using the model of Passut & Danner (see chapter 3):
the parameters are found in the database:
| Component | 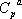 |
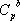 |
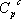 |
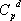 |
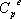 |
|---|---|---|---|---|---|
| n-dodecane | 6.35E+01 | 8.51E-01 | -2.09E-04 | -1.20E-07 | 5.50E-11 |
| 1-dodecene | 5.45E+01 | 8.04E-01 | -1.59E-04 | -1.65E-07 | 6.58E-11 |
| Hydrogen | 2.54E+01 | 1.94E-02 | -3.65E-05 | 3.00E-08 | -8.18E-12 |
We can now integrate
Which is equivalent to
to find the value of the equilibrium constant as a function of temperature. The result is shown in figure 1. We see that a high temperature is required in order to have a visible conversion.
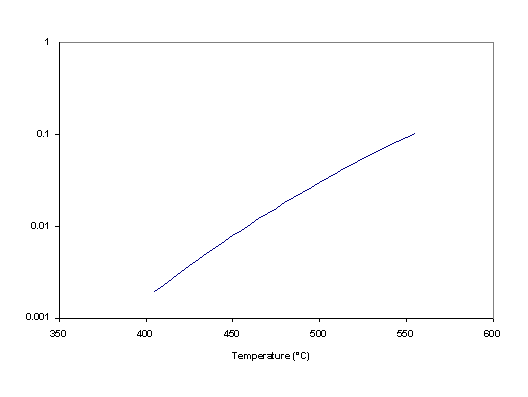 Figure 1: Equilibrium constant of the dehydrogenation of n-dodecane as a function of temperature.
Figure 1: Equilibrium constant of the dehydrogenation of n-dodecane as a function of temperature.
The mixture equilibrium composition as a function of temperature can be calculated using
and the information provided in the problem statement (the pressure is 3 bar and the molar ratio H2/HC = 6). This will yield three equations with three unknowns:
It is for example possible to calculate the conversion as:
Doing so, figure 2 is found:
 Figure 2: Effect of pressure and temperature on the n-dodecane dehydrogenation reaction.
Figure 2: Effect of pressure and temperature on the n-dodecane dehydrogenation reaction.
It is visible that increasing pressure decreases the conversion because new moles are created (the sum of the stoechiometric coefficients, 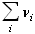 is positive). Not shown on the figure, but easy to simulate with the excel sheet, is when the hydrogen content (alpha) increases, the conversion also decreases.
is positive). Not shown on the figure, but easy to simulate with the excel sheet, is when the hydrogen content (alpha) increases, the conversion also decreases.