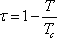Chapter 3:
From Components
to Models
Abstract
Read the abstractTable of contents
See the table of contentsList of examples
- 3-1: Vapour pressure predictions of methane using different formulas
- 3-2: Quality evaluation of molar volume correlations
- 3-3: Evaluation of the ideal gas heat capacity equations for n-pentane
- 3-4: Quality evaluation of vapourisation enthalpy correlations
- 3-5: Comparison of second virial coefficient calculation methods
- 3-6: Comparison of critical points and acentric factor from different databases
- 3-7: Use of the group contribution methods of Joback and Gani
- 3.8: Diesel fuel characterization
- 3.9: Vapour pressures of di-alcohols
- 3.10: Find the parameters to fit the vapour pressure of ethyl oleate
- 3.11: Fitting of BIP coefficients for the mixture water + MEA with the NRTL model
- 3.12: Separation of n-butane from 1,3 butadiene at 333.15K using vapour-liquid equilibrium
- 3.13: Draw the heteroazeotropic isothermal phase diagram of the binary mixture of water and butanol at 373.15 K
- 3.14: Isothermal phase diagram using the Flory Huggins activity coefficient model
- 3.15: Use of an equation of state for pure component vapour pressure calculations
Example 3-1: Vapour pressure predictions of methane using different formulas
Compare the results of the various correlations with the DIPPR correlation.
In the following tables, the characteristic properties necessary for the evaluation of each expression is given. Remember that the normal boiling point is measured at 101.325 kPa. The various parameters of the equations are:
| Parameters | Tc | Pc | ω | Tb | T3 | P3 |
|---|---|---|---|---|---|---|
| Value | 190.564 | 4599.0 | 0.0115478 | 111.66 | 90.694 | 11.696 |
| Parameter | A | B | C | D | E |
|---|---|---|---|---|---|
| Antoine-dimensionless, equation (3.12b) | 5.3157 | -5.3008 | -0.0063 | ||
| Antoine-API, equation (3.12) | 8.6775 | -911.234 | -6.34 | ||
| DIPPR, equation (3.13) | 38.664 | -1314.7 | -3.3373 | 3.0155E-05 | 2 |
| Wagner, equation (3.14) | -6.00435 | 1.1885 | -0.834082 | -1.22833 |
(Temperature in K - Pressure in Pa)
We recall some equations of chapter 3:
Antoine's equation:
Dimensionless Antoine's equation:
DIPPR equation:
Wagner's equation:
with
Analysis:
- Pressure and temperature are the basic properties of the system.
- Methane is a well-known light hydrocarbon.
- Phases present are vapour and liquid all along the saturation curve.
Solution:
See complete results in file (xls):
Some help on nomenclature and tips to use this file can be found here.
Tables for each equation are constructed and compared with the DIPPR set of calculated values. Note that the DIPPR equation does not predict exactly the critical point, the normal bubble point and the triple point; there are relative deviations around 0.2 to 0.6 %. Additionally, the acentric factor (‘omega point’ shown in figure 1) predicted by this equation is not exactly the same as that given in the database.
Relative differences are plotted in figure 1 over the full temperature range, from triple point to critical point for six different equations:
- the 3 points equation (3.11) that uses critical point, normal boiling point and triple point;
- the 2 points equation (3.8) that uses the critical point and the triple point. Note that the Wilson equation is identical but uses the critical point and the ‘omega point’. It is not shown in figure 1.
- The corresponding states equations of Ambrose (equation 3.16) and Lee-Kesler (equation (3.17) are also shown: they provide almost identical results above the ‘omega point’, but the more complex Ambrose equation extrapolates better to low reduced temperatures.
- The Antoine equation (3.12) is used either with a regression over the entire temperature domain, or using the parameters that are recommended by API Riazi (2005), but no validity range is associated with it It is clear that the difference becomes very high beyond 150 K, clearly indicating that this equation must be used only over the range 90-140 K.
- The Wagner equation (3.14) is not shown in the plot. It behaves very well if fitted on the entire temperature range.
 Figure 1: Precision of various equations for the vapour pressure of methane against the DIPPR equation.
Figure 1: Precision of various equations for the vapour pressure of methane against the DIPPR equation.
An additional curve (not shown in the book) can be constructed based on a basic formulation (Antoine's equation in this application but any other expression can be used). In this case, the parameter C is a parameter to be optimized while A and B have to satisfy the equations on 2 selected points (for example triple and critical points). Thus, the following equations have to be solved:
We find that:
Both parameters can be automatically determined once the value of C is fixed. Then an error minimization procedure can be executed on parameter C to obtain the optimum value while satisfying the restriction criteria.
References
R. L. Rowley, W. V. Wilding, J. L. Oscarson, Y. Yang, N. A. Zundel, T. E. Daubert, R. P. Danner, DIPPR® Data Compilation of Pure Compound Properties, Design Institute for Physical Properties, AIChE, New York, NY (2003).
Riazi, M. R. Characterization and Properties of Petroleum Fluids; American Society for Testing and Materials: Philadelphia, 2005.