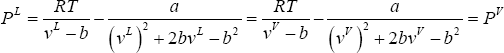Chapter 3:
From Components
to Models
Abstract
Read the abstractTable of contents
See the table of contentsList of examples
- 3-1: Vapour pressure predictions of methane using different formulas
- 3-2: Quality evaluation of molar volume correlations
- 3-3: Evaluation of the ideal gas heat capacity equations for n-pentane
- 3-4: Quality evaluation of vapourisation enthalpy correlations
- 3-5: Comparison of second virial coefficient calculation methods
- 3-6: Comparison of critical points and acentric factor from different databases
- 3-7: Use of the group contribution methods of Joback and Gani
- 3.8: Diesel fuel characterization
- 3.9: Vapour pressures of di-alcohols
- 3.10: Find the parameters to fit the vapour pressure of ethyl oleate
- 3.11: Fitting of BIP coefficients for the mixture water + MEA with the NRTL model
- 3.12: Separation of n-butane from 1,3 butadiene at 333.15K using vapour-liquid equilibrium
- 3.13: Draw the heteroazeotropic isothermal phase diagram of the binary mixture of water and butanol at 373.15 K
- 3.14: Isothermal phase diagram using the Flory Huggins activity coefficient model
- 3.15: Use of an equation of state for pure component vapour pressure calculations
Example 3-15: Use of an equation of state for a pure component vapour pressure calculation
What equations must be solved to calculate a pure component vapour pressure using an equation of state? What are the consequences on the PV plot?
This example is worked out using the Peng-Robinson equation of state (PR-EoS) with benzene, characterized as given in table 1:
| Tc (K) | Pc (Pa) | Acentric factor |
|---|---|---|
| 562.16 | 4898000 | 0.210817 |
The vapour pressure at 530 K is looked for.
Analysis:
Two conditions must be satisfied simultaneously:
- To reach mechanical equilibrium the pressure must be identical in both phases. This must be expressed explicitly, since the equation of state is pressure explicit. Hence, we state:
or for the PR- EoS:
where
 is the molar volume (all quantities are expressed as molar quantities).
is the molar volume (all quantities are expressed as molar quantities). - Chemical equilibrium is reached when the Gibbs energies are equal in both phases (chemical potentials are equal to the molar Gibbs energies for pure components):
Note that at equilibrium, liquid and vapour have the same pressure and temperature, and that the ideal gas contribution to the value of is therefore identical. It is sufficient to consider the residual contribution which is calculated using the PR-EoS as follows (for a pure component):
where  is the compressibility factor. In other words, we must find:
is the compressibility factor. In other words, we must find:
Solution:
See complete results in file (xls):
Some help on nomenclature and tips to use this file can be found here.
The PV plot of a number of isotherms, as calculated with the equation of state, is shown in figure 1.
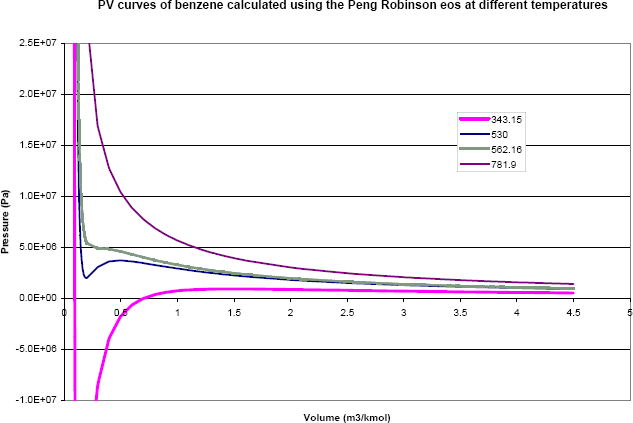 Figure 1: P-v plot of various isotherms calculated for benzene with the PR-EoS.
Figure 1: P-v plot of various isotherms calculated for benzene with the PR-EoS.
The mathematical behaviour can be analysed as follows in terms of the physical picture it should represent: the low and high molar volume limits show the liquid and vapour behaviour of the fluid (the liquid is almost incompressible and the vapour behaves according to the ideal gas law).
At intermediate volumes (and subcritical temperatures), an unphysical section is observed, that features a positive slope (negative isothermal compressibility coefficient). This is where in the physical picture a phase change will occur.
We also note that at very low temperature, a negative pressure can be found. Obviously, this is not physical either and the section of the curve that behaves that way is also in the liquid-vapour equilibrium zone.
In order to solve phase equilibrium calculation, the two equations shown above (in the ‘analysis’ section) should be solved simultaneously, using vL and vV as variables. In practice, we can proceed as follows:
- pick a pressure, P
- find, for that pressure, all volumes provided by the EoS (3 solutions if subcritical, one solution if supercritical)
- calculate the residual Gibbs energy (equivalent to the fugacity coefficient) for each of these volumes
Doing so, at the temperature of interest (530 K), figure 2 is found.
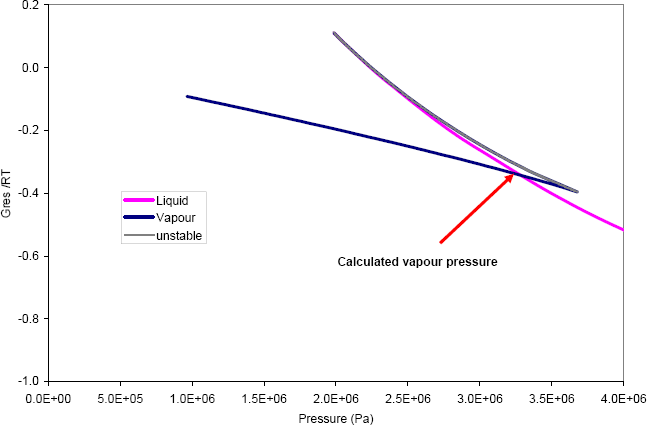 Figure 2: Solution of the vapour pressure calculation of benzene at 530 K, using the PR-EoS.
Figure 2: Solution of the vapour pressure calculation of benzene at 530 K, using the PR-EoS.
Figure 2 shows that at low pressure (until approximately 2 MPa), a single volume root is found for the equation. This volume is a vapour, and the calculated Gibbs energy is that of the vapour phase. Between 2MPa and 3.7 MPa, three volume roots are found. They can be labelled according to their size: the smallest is liquid, the largest is vapour and the intermediate is unstable. The liquid and the vapour Gibbs energy cross at the pressure P = 3.28 MPa, which is the vapour pressure that is the solution of the problem.
One can notice on figure 2 that throughout the figure, the lowest value for the Gibbs energy is that of the stable phase: vapour at low pressure, liquid at high pressure. This is in accordance with the stability principle that the Gibbs energy at fixed pressure and temperature should always be as low as possible.