Chapter 3:
From Components
to Models
Abstract
Read the abstractTable of contents
See the table of contentsList of examples
- 3-1: Vapour pressure predictions of methane using different formulas
- 3-2: Quality evaluation of molar volume correlations
- 3-3: Evaluation of the ideal gas heat capacity equations for n-pentane
- 3-4: Quality evaluation of vapourisation enthalpy correlations
- 3-5: Comparison of second virial coefficient calculation methods
- 3-6: Comparison of critical points and acentric factor from different databases
- 3-7: Use of the group contribution methods of Joback and Gani
- 3.8: Diesel fuel characterization
- 3.9: Vapour pressures of di-alcohols
- 3.10: Find the parameters to fit the vapour pressure of ethyl oleate
- 3.11: Fitting of BIP coefficients for the mixture water + MEA with the NRTL model
- 3.12: Separation of n-butane from 1,3 butadiene at 333.15K using vapour-liquid equilibrium
- 3.13: Draw the heteroazeotropic isothermal phase diagram of the binary mixture of water and butanol at 373.15 K
- 3.14: Isothermal phase diagram using the Flory Huggins activity coefficient model
- 3.15: Use of an equation of state for pure component vapour pressure calculations
Example 3-11: Fitting of BIP coefficients for the mixture water + MEA with the NRTL model
The vapour-liquid equilibrium of water + monoethanolamine (MEA) is discussed here. This example is of great practical use for CO2 capture from exhaust gases of power stations. Amine losses in the process can be controlled through accurate knowledge of the vapour-liquid equilibrium behaviour.
Analysis
The properties to be calculated are vapour-liquid equilibria.
The system is strongly non-ideal and subcritical. Pressure is considered low.
The model chosen here is the NRTL activity coefficient model. The vapour-liquid equilibrium calculation is then a heterogeneous symmetric approach: the vapour pressures (pure component liquid fugacities) of the pure components are calculated using a correlation that has been validated and that will not be further analysed here.
Solution
The parameters to be adjusted are first identified: the NRTL model contains three adjustable parameters for every pair of components ( ,
,  and
and  ). It is well known that if temperature extrapolations are needed, which is the case here, these parameters should be considered as a function of temperature, thus doubling the number of adjustable parameters. In order to limit the number of adjustable parameters, we decided in this case to fix
). It is well known that if temperature extrapolations are needed, which is the case here, these parameters should be considered as a function of temperature, thus doubling the number of adjustable parameters. In order to limit the number of adjustable parameters, we decided in this case to fix 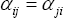 =0.2. The other two parameters are functions of temperature according to:
=0.2. The other two parameters are functions of temperature according to:
Second, the database is identified. There is a large vapour-liquid database for the binary system under consideration. It can be summarised in table 1. This database must be split into a training set and a validation set (the other data not selected in the training). For the purpose of this example, several such combinations are chosen (fit 1-4)
| Dataset reference |
Temperature (K) |
Data type |
Number of data points |
Source | Fit 1 | Fit 2 | Fit 3 | Fit 4 |
|---|---|---|---|---|---|---|---|---|
| a | 298.15 | TPx (VLE) | 15 | [1] | X | X | X | X |
| b | 323.15 | TPx (VLE) | 13 | [2] | X | X | ||
| c | 298.15 | HE | 67 | [1, 3, 4] | X | X | ||
| d | 363.15 | TPx (VLE) | 20 | [5, 6] | X | |||
| e | 308.15-573.15 | TPx (VLE) | 130 | various [7] | X |
The objective functions are determined as a function of the available data. For sets a, b, d and e (TPx data type), it is: 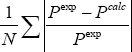
The objective function for set c is 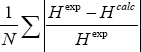
The resulting parameters can now be presented in the following regression table. Four different regressions have been performed, yielding four different parameter sets. The objective function of the different regressions contained various types of data, as indicated by the bold values in the regression table.
| Fit 1 | Fit 2 | Fit 3 | Fit 4 | |
|---|---|---|---|---|
| A12 | 1.279 | -1.894 | 8.049 | -0.01599 |
| B12 | - | 419.1 | -2019 | 7.561 |
| A21 | -1.774 | 3.869 | -2.479 | 1.693 |
| A21 | - | -1338 | 210.3 | -828.4 |
| Deviations | ||||
| a | 4.6 | 7.1 | 4.6 | 5.2 |
| b | 7.1 | 5.2 | 2.1 | 2.9 |
| c | * | 2.8 | 11.5 | 3.9 |
| d | 9.3 | 2.9 | 2.8 | 2.6 |
| e | 13.1 | 6.6 | 7.3 | 5.7 |
*: In the case of fit 1, no mixing enthalpy calculations can be performed since the parameters are independent of temperature
It is interesting to note that fit 3 which uses data at 298.15 K and 333.15 K is unable to represent the heat of mixing correctly (dataset c: AAD of 11.5 %).
Obviously the best results are obtained in fit 4, where the four datasets a, b, c and d have been used. Simultaneously, no data is available for testing.
Note nevertheless that fit 2 that uses heat of mixing data (dataset b), and only one VLE isotherm (dataset a) is able to correctly represent all other isotherms: it provides a representation close to that of fit 4.
The comparison between calculations and data is presented graphically in figure 1.
 Figure 1: VLE behaviour of the water + monoethanolamine binary mixture at 363.15 K and model behaviour using the various fits of table.
Figure 1: VLE behaviour of the water + monoethanolamine binary mixture at 363.15 K and model behaviour using the various fits of table.
A similar observation has already been made by Renon et al. (1971 [8]) who concluded that the use of mixing enthalpies greatly improves the capacity of the model for temperature extrapolations.
A second conclusion of this example is related to the numerical values of the parameters. The NRTL model is known to lead to energy parameters that are strongly inter-correlated. Figure 1 in fact shows that parameters 21 and 12 at 288.15 K are on a single line. Parameter sets 1 and 3 are almost identical in this representation, and all sets are correlated. The uncertainties associated with the parameters are also shown, and the results show that these uncertainties are smaller with fits 2 and 4, i.e. using mixing enthalpy data.
 Figure 2: Numerical values of the parameter τ21 and τ12 sets at 298.15 K
Figure 2: Numerical values of the parameter τ21 and τ12 sets at 298.15 K
In conclusion, if temperature extrapolation is required, data at various temperatures should be used in the fit, but the use of mixing enthalpy greatly improves the predictive capacity. This example used NRTL, but the same conclusion can be drawn for other models using the corresponding thermodynamic relationships.
References
[1] TOUHARA H., OKAZAKI S., OKINO F., TANAKA H., IKARI K., NAKANISHI K., Thermodynamic Properties of Aqueous Mixtures of Hydrophilic Compounds .2. Aminoethanol and Its Methyl-Derivatives, Journal of Chemical Thermodynamics, 1982, 14, n°2, p. 145-156. http://dx.doi.org/10.1016/0021-9614(82)90026-X
[2] NATH A., BENDER E., Isothermal Vapor Liquid Equilibria of Binary and Ternary Mixtures Containing Alcohol, Alkanolamine, and Water with A New Static Device, Journal of Chemical and Engineering Data, 1983, 28, n°4, p. 370-375. http://dx.doi.org/10.1021/je00034a007
[3] BUSLAEVA M.N., TSETKOV V.B., MARKOVA V.B., KAIMIN I.F., Thermochemical Study of the Donator Capability of Monoethanolamine in Solutions, Koordinatsionnaya Khimiya, 1983, 9, n°6, p. 752-754.
[4] DOHNAL V., ROUX A.H., HYNEK V., Limiting Partial Molar Excess-Enthalpies by Flow Calorimetry - Some Organic-Solvents in Water, Journal of Solution Chemistry, 1994, 23, n°8, p. 889-900. http://dx.doi.org/10.1007/BF00972752
[5] LENARD J.L., ROUSSEAU R.W., TEJA A.S., Vapor-Liquid Equilibria for Mixtures of 2-Aminoethanol + Water, AIChE Symposium Serie, 1990, 86, n°279, p. 1-5.
[6] TOCHIGI K., AKIMOTO K., OCHI K., LIU F.Y., KAWASE Y., Isothermal vapor-liquid equilibria for water+2-aminoethanol plus dimethyl sulfoxide and its constituent three binary systems, Journal of Chemical and Engineering Data, 1999, 44, n°3, p. 588-590. http://dx.doi.org/10.1021/je980068i
[7] Dechema. Detherm. [v 1.4.1.0.1]. 2005.
[8] RENON H., Local Composition in thermodynamic Excess Functions for Liquid Mixtures, AICHE.J., 1968, 14, n°1, p. 135-144. http://dx.doi.org/10.1002/aic.690140124

