Chapter 3:
From Components
to Models
Abstract
Read the abstractTable of contents
See the table of contentsList of examples
- 3-1: Vapour pressure predictions of methane using different formulas
- 3-2: Quality evaluation of molar volume correlations
- 3-3: Evaluation of the ideal gas heat capacity equations for n-pentane
- 3-4: Quality evaluation of vapourisation enthalpy correlations
- 3-5: Comparison of second virial coefficient calculation methods
- 3-6: Comparison of critical points and acentric factor from different databases
- 3-7: Use of the group contribution methods of Joback and Gani
- 3.8: Diesel fuel characterization
- 3.9: Vapour pressures of di-alcohols
- 3.10: Find the parameters to fit the vapour pressure of ethyl oleate
- 3.11: Fitting of BIP coefficients for the mixture water + MEA with the NRTL model
- 3.12: Separation of n-butane from 1,3 butadiene at 333.15K using vapour-liquid equilibrium
- 3.13: Draw the heteroazeotropic isothermal phase diagram of the binary mixture of water and butanol at 373.15 K
- 3.14: Isothermal phase diagram using the Flory Huggins activity coefficient model
- 3.15: Use of an equation of state for pure component vapour pressure calculations
Example 3-12: Separation of n-butane from 1,3-butadiene at 333.15 K using vapour-liquid equilibrium
Find a component that will enhance the separation between these two components (n-butane and 1,3-butadiene).
Analysis:
The physical property used for separation by vapour-liquid equilibrium is the volatility of the components. The vapour pressures of the pure components are the most fundamental piece of information related to volatilities. They can be found in many databases. For example, at 60°C, the vapour pressures of the two components are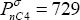 
and 
respectively (source DIPPR).
These two values are fairly close to each other. Taking into account non-idealities, we can determine (using the NRTL activity coefficient model, for example) that the infinite dilution activity coefficients are very close to one (
), indicating an almost ideal mixture. The separation of the two components by distillation will be very difficult.
In order to improve the separation, a solvent can be found in which the activity coefficients of both components are quite different. This solvent should, in addition, remain in the liquid phase to be effective, in other words have a low vapour pressure.
Solution:
Using a large database of vapour pressure data, we find that acetonitrile (CH3CN), for example, has a boiling pressure at 333.15 K of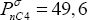 
, much lower than that of the two components to be separated, which means that it will preferentially stay in the liquid phase, where the non-idealities are stronger.
The two activity coefficients at infinite dilution of acetonitrile in butane and butadiene are respectively 
and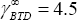 
. In other words, butadiene forms a much less non-ideal mixture with acetonitrile than n-butane. Butane has in fact no polar nature at all, while the double bonds of the butadiene result in a polarity that makes it more similar to acetonitrile. The consequences on the volatilities is made visible in figure 1, which shows that the resulting distribution coefficient of n-butane and 1,3 butadiene are both large (i.e. they are preferentially in the vapour phase), and different (i.e. they can now be separated). The acetonitrile distribution coefficient is small (<1), indicating that it remains preferentially in the liquid phase.
Figure 1: Acetonitrile as an extractive solvent for the n-butane + 1,3-butadiene mixture. The plot shows the distribution coefficient of the components at 333.15 K and the bubble pressure.